Wikipedia
This text was copied from Wikipedia on 18 January 2025 at 6:10AM.
John Wallis | |
|---|---|
 | |
| Born | 3 December [O.S. 23 November] 1616 Ashford, Kent, England |
| Died | 8 November 1703(1703-11-08) (aged 86) [O.S. 28 October 1703] Oxford, Oxfordshire, England |
| Nationality | English |
| Education | Felsted School, Emmanuel College, Cambridge |
| Known for | Wallis product Inventing the symbol ∞ Extending Cavalieri's quadrature formula Coining the term "momentum"[1] |
| Spouse | Susanna Glynde (m. 1645) |
| Children | 3, including Anne, Lady Blencowe |
| Scientific career | |
| Fields | Mathematics |
| Institutions | |
| Academic advisors | William Oughtred |
| Notable students | William Brouncker |
John Wallis (/ˈwɒlɪs/;[2] Latin: Wallisius; 3 December [O.S. 23 November] 1616 – 8 November [O.S. 28 October] 1703) was an English clergyman and mathematician, who is given partial credit for the development of infinitesimal calculus.
Between 1643 and 1689 Wallis served as chief cryptographer for Parliament and, later, the royal court.[3] He is credited with introducing the symbol ∞ to represent the concept of infinity.[4] He similarly used 1/∞ for an infinitesimal. He was a contemporary of Newton and one of the greatest intellectuals of the early renaissance of mathematics.[5]
Biography
Educational background
- Cambridge, M.A., Oxford, D.D.
- Grammar School at Tenterden, Kent, 1625–31.
- School of Martin Holbeach at Felsted, Essex, 1631–2.
- Cambridge University, Emmanuel College, 1632–40; B.A., 1637; M.A., 1640.
- D.D. at Oxford in 1654.
Family
On 14 March 1645, he married Susanna Glynde (c. 1600 – 16 March 1687). They had three children:
- Anne, Lady Blencowe (4 June 1656 – 5 April 1718), married Sir John Blencowe (30 November 1642 – 6 May 1726) in 1675, with issue[6]
- John Wallis (26 December 1650 – 14 March 1717),[7] MP for Wallingford 1690–1695, married Elizabeth Harris (d. 1693) on 1 February 1682, with issue: one son and two daughters
- Elizabeth Wallis (1658–1703[8]), married William Benson (1649–1691) of Towcester, died with no issue
Life
This section needs additional citations for verification. (April 2024) |
John Wallis was born in Ashford, Kent. He was the third of five children of Revd. John Wallis and Joanna Chapman. He was initially educated at a school in Ashford but moved to James Movat's school in Tenterden in 1625 following an outbreak of plague. Wallis was first exposed to mathematics in 1631, at Felsted School (then known as Martin Holbeach's school in Felsted); he enjoyed maths, but his study was erratic, since "mathematics, at that time with us, were scarce looked on as academical studies, but rather mechanical" (Scriba 1970). At the school in Felsted, Wallis learned how to speak and write Latin. By this time, he also was proficient in French, Greek, and Hebrew.[9] As it was intended he should be a doctor, he was sent in 1632 to Emmanuel College, Cambridge.[10] While there, he kept an act on the doctrine of the circulation of the blood; that was said to have been the first occasion in Europe on which this theory was publicly maintained in a disputation. His interests, however, centred on mathematics. He received his Bachelor of Arts degree in 1637 and a Master's in 1640, afterwards entering the priesthood. From 1643 to 1649, he served as a nonvoting scribe at the Westminster Assembly. He was elected to a fellowship at Queens' College, Cambridge in 1644, from which he had to resign following his marriage.
Throughout this time, Wallis had been close to the Parliamentarian party, perhaps as a result of his exposure to Holbeach at Felsted School. He rendered them great practical assistance in deciphering Royalist dispatches. The quality of cryptography at that time was mixed; despite the individual successes of mathematicians such as François Viète, the principles underlying cipher design and analysis were very poorly understood. Most ciphers were ad hoc methods relying on a secret algorithm, as opposed to systems based on a variable key. Wallis realised that the latter were far more secure – even describing them as "unbreakable", though he was not confident enough in this assertion to encourage revealing cryptographic algorithms. He was also concerned about the use of ciphers by foreign powers, refusing, for example, Gottfried Leibniz's request of 1697 to teach Hanoverian students about cryptography.[11]
Returning to London – he had been made chaplain at St Gabriel Fenchurch in 1643 – Wallis joined the group of scientists that was later to evolve into the Royal Society. He was finally able to indulge his mathematical interests, mastering William Oughtred's Clavis Mathematicae in a few weeks in 1647. He soon began to write his own treatises, dealing with a wide range of topics, which he continued for the rest of his life. Wallis wrote the first survey about mathematical concepts in England where he discussed the Hindu-Arabic system.[12]
Wallis joined the moderate Presbyterians in signing the remonstrance against the execution of Charles I, by which he incurred the lasting hostility of the Independents. In spite of their opposition he was appointed in 1649 to the Savilian Chair of Geometry at Oxford University, where he lived until his death on 8 November [O.S. 28 October] 1703. In 1650, Wallis was ordained as a minister. After, he spent two years with Sir Richard Darley and Lady Vere as a private chaplain. In 1661, he was one of twelve Presbyterian representatives at the Savoy Conference.
Besides his mathematical works he wrote on theology, logic, English grammar and philosophy, and he was involved in devising a system for teaching a deaf boy to speak at Littlecote House.[13] William Holder had earlier taught a deaf man, Alexander Popham, to speak "plainly and distinctly, and with a good and graceful tone".[14] Wallis later claimed credit for this, leading Holder to accuse Wallis of "rifling his Neighbours, and adorning himself with their spoyls".[15]
Wallis' appointment as Savilian Professor of Geometry at the Oxford University
The Parliamentary visitation of Oxford, that began in 1647, removed many senior academics from their positions, including in November 1648, the Savilian Professors of Geometry and Astronomy. In 1649 Wallis was appointed as Savilian Professor of Geometry. Wallis seems to have been chosen largely on political grounds (as perhaps had been his Royalist predecessor Peter Turner, who despite his appointment to two professorships never published any mathematical works); while Wallis was perhaps the nation's leading cryptographer and was part of an informal group of scientists that would later become the Royal Society, he had no particular reputation as a mathematician. Nonetheless, Wallis' appointment proved richly justified by his subsequent work during the 54 years he served as Savilian Professor.[16]
Contributions to mathematics

Wallis made significant contributions to trigonometry, calculus, geometry, and the analysis of infinite series. In his Opera Mathematica I (1695) he introduced the term "continued fraction".
Analytic geometry
In 1655, Wallis published a treatise on conic sections in which they were defined analytically. This was the earliest book in which these curves are considered and defined as curves of the second degree. It helped to remove some of the perceived difficulty and obscurity of René Descartes' work on analytic geometry.
In Treatise on the Conic Sections, Wallis popularised the symbol ∞ for infinity. He wrote, "I suppose any plane (following the Geometry of Indivisibles of Cavalieri) to be made up of an infinite number of parallel lines, or as I would prefer, of an infinite number of parallelograms of the same altitude; (let the altitude of each one of these be an infinitely small part 1/∞ of the whole altitude, and let the symbol ∞ denote Infinity) and the altitude of all to make up the altitude of the figure."[17]
Integral calculus
Arithmetica Infinitorum, the most important of Wallis's works, was published in 1656. In this treatise the methods of analysis of Descartes and Cavalieri were systematised and extended, but some ideas were open to criticism. He began, after a short tract on conic sections, by developing the standard notation for powers, extending them from positive integers to rational numbers:
-
x
0
=
1
{\displaystyle x^{0}=1}
-
x
−
1
=
1
x
{\displaystyle x^{-1}={\frac {1}{x}}}
-
x
−
n
=
1
x
n
etc.
{\displaystyle x^{-n}={\frac {1}{x^{n}}}{\text{ etc.}}}
-
x
1
/
2
=
x
{\displaystyle x^{1/2}={\sqrt {x}}}
-
x
2
/
3
=
x
2
3
etc.
{\displaystyle x^{2/3}={\sqrt[{3}]{x^{2}}}{\text{ etc.}}}
-
x
1
/
n
=
x
n
{\displaystyle x^{1/n}={\sqrt[{n}]{x}}}
-
x
p
/
q
=
x
p
q
{\displaystyle x^{p/q}={\sqrt[{q}]{x^{p}}}}
Leaving the numerous algebraic applications of this discovery, he next proceeded to find, by integration, the area enclosed between the curve y = xm, x-axis, and any ordinate x = h, and he proved that the ratio of this area to that of the parallelogram on the same base and of the same height is 1/(m + 1), extending Cavalieri's quadrature formula. He apparently assumed that the same result would be true also for the curve y = axm, where a is any constant, and m any number positive or negative, but he discussed only the case of the parabola in which m = 2 and the hyperbola in which m = −1. In the latter case, his interpretation of the result is incorrect. He then showed that similar results may be written down for any curve of the form
-
y
=
∑
m
a
x
m
{\displaystyle y=\sum _{m}^{}ax^{m}}
and hence that, if the ordinate y of a curve can be expanded in powers of x, its area can be determined: thus he says that if the equation of the curve is y = x0 + x1 + x2 + ..., its area would be x + x2/2 + x3/3 + ... . He then applied this to the quadrature of the curves y = (x − x2)0, y = (x − x2)1, y = (x − x2)2, etc., taken between the limits x = 0 and x = 1. He shows that the areas are, respectively, 1, 1/6, 1/30, 1/140, etc. He next considered curves of the form y = x1/m and established the theorem that the area bounded by this curve and the lines x = 0 and x = 1 is equal to the area of the rectangle on the same base and of the same altitude as m : m + 1. This is equivalent to computing
-
∫
0
1
x
1
/
m
d
x
.
{\displaystyle \int _{0}^{1}x^{1/m}\,dx.}
He illustrated this by the parabola, in which case m = 2. He stated, but did not prove, the corresponding result for a curve of the form y = xp/q.
Wallis showed considerable ingenuity in reducing the equations of curves to the forms given above, but, as he was unacquainted with the binomial theorem, he could not effect the quadrature of the circle, whose equation is
y
=
1
−
x
2
{\displaystyle y={\sqrt {1-x^{2}}}}






-
∫
0
1
(
1
−
x
2
)
0
d
x
and
∫
0
1
(
1
−
x
2
)
1
d
x
,
{\displaystyle \int _{0}^{1}(1-x^{2})^{0}\,dx\ {\text{ and }}\int _{0}^{1}(1-x^{2})^{1}\,dx,}
that is,
1
{\displaystyle 1}






-
π
2
=
2
1
⋅
2
3
⋅
4
3
⋅
4
5
⋅
6
5
⋅
6
7
⋯
{\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdots }
(which is now known as the Wallis product).
In this work the formation and properties of continued fractions are also discussed, the subject having been brought into prominence by Brouncker's use of these fractions.
A few years later, in 1659, Wallis published a tract containing the solution of the problems on the cycloid which had been proposed by Blaise Pascal. In this he incidentally explained how the principles laid down in his Arithmetica Infinitorum could be used for the rectification of algebraic curves and gave a solution of the problem to rectify (i.e., find the length of) the semicubical parabola x3 = ay2, which had been discovered in 1657 by his pupil William Neile. Since all attempts to rectify the ellipse and hyperbola had been (necessarily) ineffectual, it had been supposed that no curves could be rectified, as indeed Descartes had definitely asserted to be the case. The logarithmic spiral had been rectified by Evangelista Torricelli and was the first curved line (other than the circle) whose length was determined, but the extension by Neile and Wallis to an algebraic curve was novel. The cycloid was the next curve rectified; this was done by Christopher Wren in 1658.
Early in 1658 a similar discovery, independent of that of Neile, was made by van Heuraët, and this was published by van Schooten in his edition of Descartes's Geometria in 1659. Van Heuraët's method is as follows. He supposes the curve to be referred to rectangular axes; if this is so, and if (x, y) are the coordinates of any point on it, and n is the length of the normal, and if another point whose coordinates are (x, η) is taken such that η : h = n : y, where h is a constant; then, if ds is the element of the length of the required curve, we have by similar triangles ds : dx = n : y. Therefore, h ds = η dx. Hence, if the area of the locus of the point (x, η) can be found, the first curve can be rectified. In this way van Heuraët effected the rectification of the curve y3 = ax2 but added that the rectification of the parabola y2 = ax is impossible since it requires the quadrature of the hyperbola. The solutions given by Neile and Wallis are somewhat similar to that given by van Heuraët, though no general rule is enunciated, and the analysis is clumsy. A third method was suggested by Fermat in 1660, but it is inelegant and laborious.
Collision of bodies
The theory of the collision of bodies was propounded by the Royal Society in 1668 for the consideration of mathematicians. Wallis, Christopher Wren, and Christiaan Huygens sent correct and similar solutions, all depending on what is now called the conservation of momentum; but, while Wren and Huygens confined their theory to perfectly elastic bodies (elastic collision), Wallis considered also imperfectly elastic bodies (inelastic collision). This was followed in 1669 by a work on statics (centres of gravity), and in 1670 by one on dynamics: these provide a convenient synopsis of what was then known on the subject.
Algebra
In 1685 Wallis published Algebra, preceded by a historical account of the development of the subject, which contains a great deal of valuable information. The second edition, issued in 1693 and forming the second volume of his Opera, was considerably enlarged. This algebra is noteworthy as containing the first systematic use of formulae. A given magnitude is here represented by the numerical ratio which it bears to the unit of the same kind of magnitude: thus, when Wallis wants to compare two lengths he regards each as containing so many units of length. This perhaps will be made clearer by noting that the relation between the space described in any time by a particle moving with a uniform velocity is denoted by Wallis by the formula
- s = vt,
where s is the number representing the ratio of the space described to the unit of length; while the previous writers would have denoted the same relation by stating what is equivalent to the proposition
- s1 : s2 = v1t1 : v2t2.
Number line
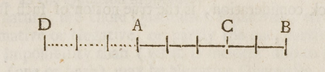
 , Wallis wrote in A treatise of algebra that "...
−
3
{\displaystyle -3}
, Wallis wrote in A treatise of algebra that "...
−
3
{\displaystyle -3}
 doth as truly design the Point
D
{\displaystyle D}
doth as truly design the Point
D
{\displaystyle D}
 ; as
+
3
{\displaystyle +3}
; as
+
3
{\displaystyle +3}
 designed the Point
C
{\displaystyle C}
designed the Point
C
{\displaystyle C}
 ... And each designs (at least in the same Infinite Line) one Single Point: And but one."
... And each designs (at least in the same Infinite Line) one Single Point: And but one."Wallis has been credited as the originator of the number line "for negative quantities"[18] and "for operational purposes."[19] This is based on a passage in his 1685 treatise on algebra in which he introduced a number line to illustrate the legitimacy of negative quantities:[20]
Yet is not that Supposition (of Negative Quantities) either Unuseful or Absurd; when rightly understood. And though, as to the bare Algebraick Notation, it import a Quantity less than nothing: Yet, when it comes to a Physical Application, it denotes as Real a Quantity as if the Sign were + {\displaystyle +}
; but to be interpreted in a contrary sense... + 3 {\displaystyle +3}
, signifies 3 {\displaystyle 3}
Yards Forward; and − 3 {\displaystyle -3}
, signifies 3 {\displaystyle 3}
Yards Backward.
It has been noted that, in an earlier work, Wallis came to the conclusion that the ratio of a positive number to a negative one is greater than infinity. The argument involves the quotient
1
x
{\displaystyle {\tfrac {1}{x}}}





Geometry
He is usually credited with the proof of the Pythagorean theorem using similar triangles. However, Thabit Ibn Qurra (AD 901), an Arab mathematician, had produced a generalisation of the Pythagorean theorem applicable to all triangles six centuries earlier. It is a reasonable conjecture that Wallis was aware of Thabit's work.[22]
Wallis was also inspired by the works of Islamic mathematician Sadr al-Tusi, the son of Nasir al-Din al-Tusi, particularly by al-Tusi's book written in 1298 on the parallel postulate. The book was based on his father's thoughts and presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. After reading this, Wallis then wrote about his ideas as he developed his own thoughts about the postulate, trying to prove it also with similar triangles.[23]
He found that Euclid's fifth postulate is equivalent to the one currently named "Wallis postulate" after him. This postulate states that "On a given finite straight line it is always possible to construct a triangle similar to a given triangle". This result was encompassed in a trend trying to deduce Euclid's fifth from the other four postulates which today is known to be impossible. Unlike other authors, he realised that the unbounded growth of a triangle was not guaranteed by the four first postulates.[24]
Calculator
Another aspect of Wallis's mathematical skills was his ability to do mental calculations. He slept badly and often did mental calculations as he lay awake in his bed. One night he calculated in his head the square root of a number with 53 digits. In the morning he dictated the 27-digit square root of the number, still entirely from memory. It was a feat that was considered remarkable, and Henry Oldenburg, the Secretary of the Royal Society, sent a colleague to investigate how Wallis did it. It was considered important enough to merit discussion in the Philosophical Transactions of the Royal Society of 1685.[25][26]
Musical theory
Wallis translated into Latin works of Ptolemy and Bryennius, and Porphyrius's commentary on Ptolemy. He also published three letters to Henry Oldenburg concerning tuning. He approved of equal temperament, which was being used in England's organs.[27]
Other works

His Institutio logicae, published in 1687, was very popular.[4] The Grammatica linguae Anglicanae was a work on English grammar, that remained in print well into the eighteenth century. He also published on theology.[4]
Wallis as cryptographer
While employed as lady Vere's chaplain in 1642 Wallis was given an enciphered letter about the fall of Chicester which he managed to decipher within two hours. This started his career as a cryptographer. He was a moderate supporter of the Parliamentarian side in the First English Civil War and therefore worked as a decipherer of intercepted correspondence for the Parliamentarian leaders. For his services he was rewarded with the Livings of St. Gabriel and St. Martin's in London.[28]
Because of his Parliamentarian sympathies Wallis was not employed as a cryptographer after the Stuart Restoration,[29] but after the Glorious Revolution he was sought out by lord Nottingham and frequently employed to decipher encrypted intercepted correspondence, though he thought that he was not always adequately rewarded for his work.[a] King William III from 1689 also employed Wallis as a cryptographer, sometimes almost on a daily basis. Couriers would bring him letters to be decrypted and waited in front of his study for the product. The king took a personal interest in Wallis' work and well-being as witnessed by a letter he sent to Dutch Grand pensionary Anthonie Heinsius in 1689.[29]
In these early days of the Williamite reign directly obtaining foreign intercepted letters was a problem for the English, as they did not have the resources of foreign Black Chambers as yet, but allies like the Elector of Brandenburg without their own Black Chambers occasionally made gifts of such intercepted correspondence, like the letter of king Louis XIV of France to king John III Sobieski of Poland that king William in 1689 used to cause a crisis in French-Polish diplomatic relations. He was quite open about it and Wallis was rewarded for his role.[31] But Wallis became nervous that the French might take action against him.[32]
Wallis relationship with the German mathematician Gottfried Wilhelm Leibniz was cordial. But Leibniz also had cryptographic interests and tried to get Wallis to divulge some of his trade secrets, which Wallis declined to do as a matter of patriotic principle.[33]
Smith gives an example of the painstaking work that Wallis performed, as described by himself in a letter to Richard Hampden of 3 August 1689. In it he gives a detailed account of his work on a particular letter and the parts he had encountered difficulties with.[34]
Wallis' correspondence also shows details of the way he stood up for himself, when he thought he was under-appreciated, financially or otherwise. He lobbied enthusiastically, both on his own behalf, and that of his relatives, as witnessed by letters to Lord Nottingham, Richard Hampden and the MP Harbord Harbord that Smith quotes.[35] In a letter to the English envoy to Prussia, James Johnston Wallis bitterly complains that a courtier of the Prussian Elector, by the name of Smetteau, had done him wrong in the matter of just compensation for services rendered to the Elector. In the letter he gives details of what he had done and gives advice on a simple substitution cipher for the use of Johnston himself.[36]
Wallis' contributions to the art of cryptography were not only of a "technological" character. De Leeuw points out that even the "purely scientific" contributions of Wallis to the science of linguistics in the field of the "rationality" of Natural language as it developed over time, played a role in the development of cryptology as a science. Wallis' development of a model of English grammar, independent of earlier models based on Latin grammar, is a case in point of the way other sciences helped develop cryptology in his view.[37]
Wallis tried to teach his own son John, and his grandson by his daughter Anne, William Blencowe the tricks of the trade. With William he was so successful that he could persuade the government to allow the grandson to get the survivorship of the annual pension of £100 Wallis had received in compensation for his cryptographic work.[38]
William Blencowe eventually succeeded Wallis as official Cryptographer to Queen Anne after Wallis' death in 1703.[39]
See also
- 31982 Johnwallis, an asteroid that was named after him
- Invisible College
- John Wallis Academy – former ChristChurch school in Ashford renamed in 2010
- Wallis's conical edge
- Wallis' integrals
Notes
References
- ^ Joseph Frederick Scott, The mathematical work of John Wallis (1616-1703), Taylor and Francis, 1938, p. 109.
- ^ Random House Dictionary.
- ^ Smith, David Eugene (1917). "John Wallis As a Cryptographer". Bulletin of the American Mathematical Society. 24 (2): 82–96. doi:10.1090/s0002-9904-1917-03015-7. MR 1560009.
- ^ a b c Chisholm, Hugh, ed. (1911). . Encyclopædia Britannica. Vol. 28 (11th ed.). Cambridge University Press. p. 284–285.
- ^ Kearns, D. A. (1958). "John Wallis and complex numbers". The Mathematics Teacher. 51 (5): 373–374. JSTOR 27955680.
- ^ Joan Thirsk (2005). "Blencowe, Anne, Lady Blencowe (1656–1718)". Oxford Dictionary of National Biography. Oxford Dictionary of National Biography (online ed.). Oxford University Press. doi:10.1093/ref:odnb/41326. Retrieved 21 August 2023. (Subscription or UK public library membership required.)
- ^ "WALLIS, John (1650-1717), of Soundness, Nettlebed, Oxon". History of Parliament Online. Retrieved 21 August 2023.
- ^ "Elizabeth Wallis". Early Modern Letters Online : Person. Retrieved 21 August 2023.
- ^ Yule, G. Udny (1939). "John Wallis, D.D., F.R.S.". Notes and Records of the Royal Society of London. 2 (1): 74–82. doi:10.1098/rsnr.1939.0012. JSTOR 3087253.
- ^ "Wallys, John (WLS632J)". A Cambridge Alumni Database. University of Cambridge.
- ^ Kahn, David (1967), The Codebreakers: The Story of Secret Writing, New York: Macmillan, p. 169, LCCN 63016109
- ^ 4
- ^ "Find could end 350-year science dispute". BBC. 26 July 2008. Retrieved 5 May 2018.
- ^ W. Holder, W. (1668). "Of an Experiment, Concerning Deafness". Philosophical Transactions of the Royal Society 3, pp. 665–668.
- ^ Holder, Philosophical Transactions of the Royal Society, supplement, 10.
- ^ John Wallis: Time-line, maths.ox.ac.uk. Accessed 19 April 2024.
- ^ Scott, J.F. 1981. The Mathematical Work of John Wallis, D.D., F.R.S. (1616–1703). Chelsea Publishing Co., New York, NY. p. 18.
- ^ a b Heeffer, Albrecht (10 March 2011). "Historical Objections Against the Number Line". Science & Education. 20 (9): 863–880 [872–876]. Bibcode:2011Sc&Ed..20..863H. doi:10.1007/s11191-011-9349-0. hdl:1854/LU-1891046. S2CID 120058064.
- ^ Núñez, Rafael (2017). "How Much Mathematics Is "Hardwired," If Any at All: Biological Evolution, Development, and the Essential Role of Culture" (PDF). In Sera, Maria D.; Carlson, Stephanie M.; Maratsos, Michael (eds.). Minnesota Symposium on Child Psychology: Culture and Developmental Systems, Volume 38. John Wiley & Sons, Inc. pp. 83–124 [96]. doi:10.1002/9781119301981.ch3. Archived from the original (PDF) on 16 April 2022. Retrieved 16 April 2022.
- ^ Wallis, John (1685). A treatise of algebra, both historical and practical. London: Richard Davis. p. 265. MPIWG:GK8U243K.
- ^ Martínez, Alberto A. (2006). Negative Math: How Mathematical Rules Can Be Positively Bent. Princeton University Press. p. 22. ISBN 978-0-691-12309-7. Retrieved 9 June 2013.
- ^ Joseph, G.G. (2000). The Crest of the Peacock: Non-European Roots of Mathematics (2 ed.). Penguin. p. 337. ISBN 978-0-14-027778-4.
- ^ The Mathematics of Egypt, Mesopotamia, China, India, and Islam:A Sourcebook Victor J. Katz Princeton University Press Archived 1 October 2016 at the Wayback Machine
- ^ Burton, David M. (2011), The History of Mathematics / An Introduction (7th ed.), McGraw-Hill, p. 566, ISBN 978-0-07-338315-6
- ^ Dr. Wallis (1685) "Two extracts of the Journal of the Phil. Soc. of Oxford; one containing a paper, communicated March 31, 1685, by the Reverend Dr. Wallis, president of that society, concerning the strength of memory when applied with due attention; … ", Philosophical Transactions of the Royal Society of London, 15 : 1269-1271. Available on-line at: Royal Society of London
- ^ Hoppen, K. Theodore (2013), The Common Scientist of the Seventeenth Century: A Study of the Dublin Philosophical Society, 1683–1708, Routledge Library Editions: History & Philosophy of Science, vol. 15, Routledge, p. 157, ISBN 9781135028541
- ^ David Damschoder and David Russell Williams, Music Theory from Zarlino to Schenker: A Bibliography and Guide (Stytvesant, NY: Pendragon Press, 1990), p. 374.
- ^ Smith, p. 83
- ^ a b De Leeuw (1999), p. 138
- ^ Smith, pp. 83-86
- ^ Smith, p. 87
- ^ De Leeuw (1999), p. 139
- ^ Smith, pp. 83-84
- ^ Smith, pp. 85-87
- ^ Smith, pp. 89-93
- ^ Smith, pp. 94-96
- ^ De Leeuw (2000), p. 9
- ^ Cave, E., ed. (1788). "Original Letter of dr. Wallis with Some Particulars of his Pension". The Gentleman's Magazine. 63 (June 1788): 479–480. Retrieved 20 August 2023.
- ^ De Leeuw (1999), p.143
Sources
- The initial text of this article was taken from the public domain resource:
- W. W. Rouse Ball (1908). "A Short Account of the History of Mathematics" (4 ed.).
- Leeuw, K. de (1999). "The Black Chamber in the Dutch Republic during the War of the Spanish Succession and it Aftermath, 1707-1715" (PDF). The Historical Journal. 42 (1): 133–156. doi:10.1017/S0018246X98008292. S2CID 162387765. Retrieved 3 August 2023.
- Leeuw, K. de (2000). "The use of codes and ciphers in the Dutch Republic, mainly during the 18th century". Cryptology and statecraft in the Dutch Republic (PDF). Amsterdam. pp. 6–51. Retrieved 4 August 2023.
{{cite book}}: CS1 maint: location missing publisher (link) - Smith, David Eugene (1917). "John Wallis As a Cryptographer". Bulletin of the American Mathematical Society. 24 (2): 82–96. doi:10.1090/s0002-9904-1917-03015-7. MR 1560009.
- Scriba, C J (1970). "The autobiography of John Wallis, F.R.S.". Notes and Records of the Royal Society of London. 25: 17–46. doi:10.1098/rsnr.1970.0003. S2CID 145393357.
- Stedall, Jacqueline, 2005, "Arithmetica Infinitorum" in Ivor Grattan-Guinness, ed., Landmark Writings in Western Mathematics. Elsevier: 23–32.
- Guicciardini, Niccolò (2012) "John Wallis as editor of Newton's Mathematical Work", Notes and Records of the Royal Society of London 66(1): 3–17. Jstor link
- Stedall, Jacqueline A. (2001) "Of Our Own Nation: John Wallis's Account of Mathematical Learning in Medieval England", Historia Mathematica 28: 73.
- Wallis, J. (1691). A seventh letter, concerning the sacred Trinity occasioned by a second letter from W.J. / by John Wallis ... (Early English books online). London: Printed for Tho. Parkhurst ...
External links
- The Correspondence of John Wallis in EMLO
- . Dictionary of National Biography. London: Smith, Elder & Co. 1885–1900.
- O'Connor, John J.; Robertson, Edmund F., "John Wallis", MacTutor History of Mathematics Archive, University of St Andrews
- Galileo Project page
- "Archival material relating to John Wallis". UK National Archives.
- Portraits of John Wallis at the National Portrait Gallery, London
- Works by John Wallis at Post-Reformation Digital Library
- John Wallis (1685) A treatise of algebra - digital facsimile, Linda Hall Library
- Wallis, John (1685). A Treatise of Algebra, both Historical and Practical. Shewing the Original, Progress, and Advancement thereof, from time to time, and by what Steps it hath attained to the Heighth at which it now is. Oxford: Richard Davis. doi:10.3931/e-rara-8842.
- Hutchinson, John (1892). . Men of Kent and Kentishmen (Subscription ed.). Canterbury: Cross & Jackman. pp. 139–140.





![{\displaystyle x^{2/3}={\sqrt[{3}]{x^{2}}}{\text{ etc.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea7b917ee8df59ead6e27c56ce459e2761baafb9)
![{\displaystyle x^{1/n}={\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94140b99de85804d7b71ccd80aa498a9d374bdd2)
![{\displaystyle x^{p/q}={\sqrt[{q}]{x^{p}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1c8c535fff27c5351373ce819cd68f5c8e16670)






1 Annotation
Second Reading
Bill • Link
Dr. John Wallis was born at Ashford in Kent, of which parish his father was minister. After learning a little arithmetic of his brother, he made his way in the mathematics by the force of a genius which seemed to be designed by nature for this branch of science, and that was equal to every thing to which it was applied. He was not content with treading in the footsteps of other mathematicians, but in several instances went beyond them; and is by Mr. Glanvill ranked with Vieta and Des Cartes, who are of the first class of discoverers in mathematical knowledge. He invented the method for measuring all kinds of curves, and was thought to have gone nearer than any other man towards squaring the circle, which he has demonstrated to be impossible. He greatly improved decimal arithmetic, and was the first that reduced a fraction, by a continued division, to an infinite series; which series was afterwards employed by lord Brouncker in squaring the hyperbola. He was the inventor of the modern art of deciphering, which he practised in the time of the civil war. The writers of the papers which he undertook to explain, were astonished when they saw them deciphered; and fairly owned that there was great truth, if not infallibility, in his art. He was probably the first that invented a method of teaching deaf and dumb persons to speak, and to understand a language. He composed an English grammar, in which are many things entirely his own, and which shew at once the grammarian and the philosopher. Ob. 28 Oct. 1703, Æt. 87.
---A Biographical History of England. J. Granger, 1779.